Spring Constant Units Calculator
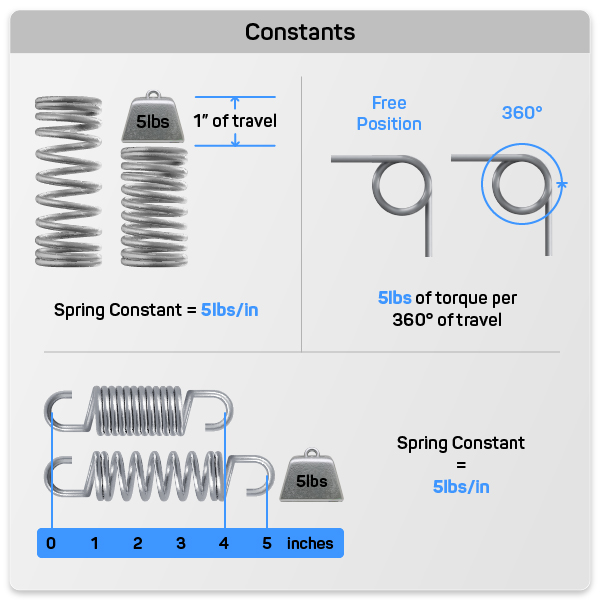
The units of measurement for the constant amount of force per unit of travel a compression or extension spring is able to exert, is measured in pounds of force per inch (lbf/in) or newtons per millimeter (N/mm). For torsion springs, the spring constant (torque) units are inch-pounds of torque per 360º (degrees) or inch-pounds of torque per degree; newtons per millimeter per 360º (degrees) or newtons per millimeter per degree in the metric system.
Compression And Extension Spring Rate
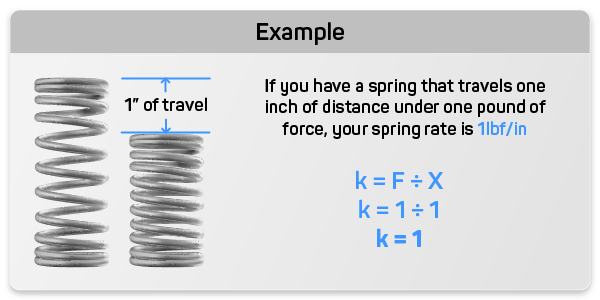
Spring constant units in extension and sspring constant offer a linear force. Spring constant k is the master of your compression or extension spring design. You must consider the load you will be applying on the spring and how much deflection or travel you expect from your spring under that load. The spring constant units for load are pounds of force (lbf) or newtons (N) in the metric system of measurement. Spring constant units for travel are inches (in) or millimeters (mm). The formulas and diagrams provided below will help you calculate your compression or extension spring’s constant.
Constant Formula A.)
To calculate how much spring constant you need.
- X = distance traveled
- F = load
- k = rate
Rate Formula B.)
To calculate spring constant of a spring.
- d = Wire Diameter
- D outer = Outer Diameter
- D = Mean Diameter
- E = Young’s Modulus of Material
- G = Shear Modulus of Material
- L free = Free Length
- k = Spring Rate (Spring Constant)
- na = Active Coils
- v = Poison’s Ratio of Material
Torsion Spring Constant
When it comes to torsion springs the force is radial. In this case, torsion spring rate is the amount of constant force or torque your torsion spring exerts per every 360 degrees of deflection (travel) or 1º degree of deflection. The formulas and diagrams provided below will help you calculate your torsion spring rate.
Torque Formula A.)
To calculate torsion spring rate per 360º (degrees).
- d = wire size (inches)
- D = Mean Diameter (inches)
- N = Number of active coils
- E = Modulus of Elasticity
- R = Rate per 360º
- R2 = Rate per Degree

Torque Formula B.)
To calculate how much torsion spring rate per degree you need.
- k2 = Rate per Degree
- X = Distance Traveled
- F = Torque or Load