search
Loading...

Spring Pitch Calculator

Compression Springs Compression Springs

Input results shown will be +/- 10% from middle value
Hint: The closer your min and max inputs are, the more accurate your results will be!

Outside Diameter
to
Inside Diameter
to
Free Length
to
Wire Diameter
to
Total Coils
to
Rate
to
Material Type
Max. Load
to
Max. Deflection
to
Solid Height
to
*Required Field
Extension Springs Extension Springs

Input results shown will be +/- 10% from middle value
Hint: The closer your min and max inputs are, the more accurate your results will be!

Outside Diameter
to
Length Inside Hook
to
Wire Diameter
to
Max. Load
to
Max. Deflection
to
Initial Tension
to
Rate
to
Material Type
*Required Field
Torsion Springs Torsion Springs

Input results shown will be +/- 10% from middle value
Hint: The closer your min and max inputs are, the more accurate your results will be!

Outside Diameter
to
Inside Diameter
to
Total Coils
to
Free Position
to
Wire Diameter
to
Body Length
to
Max. Torque
to
Max. Deflection
to
Rate
to
Leg Length
to
Material Type
*Required Field
 

Definition: Spring calculator which calculates spring pitch. Spring pitch is the distance in between a helical spring’s adjacent coils from center of wire to center of wire.

Spring pitch is a  dimension which can be difficult to calculate if the right procedures and formulas aren’t followed. Our spring calculator will calculate this value automatically but if you want to know how we’ve done it, the formulas used in the calculator to calculate spring pitch are provided below.

The calculation of spring pitch is different depending on the type of ends. Below are the formulas for the types of ends which are provided in our spring pitch calculator. These types of ends are closed and squared, closed and ground, double closed, and open ends.

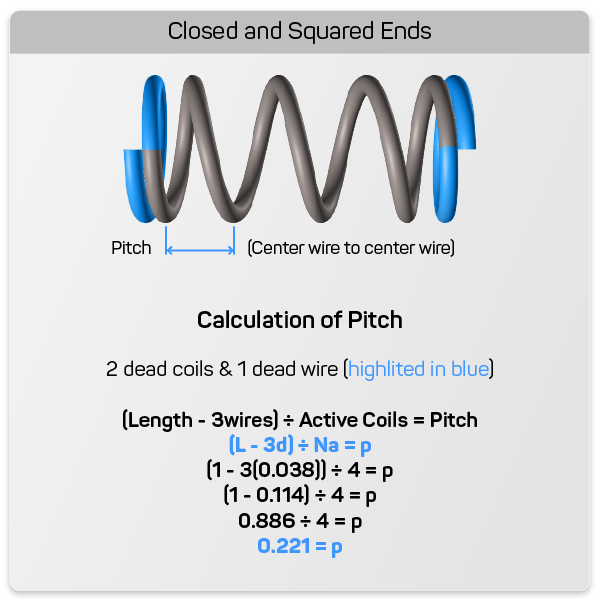
Closed and Squared

The most common type of ends. This end type has two closed coils which are inactive and therefore have no pitch in between. These are dead coils. There is also a dead wire because, since spring pitch is calculated from center of wire to center of wire, half of the last wire is also dead so if we join both halves from both ends, they make up one full wire. This means that we’ll have to subtract three wires from the free length before we divide the length by the active coils as shown in the formula below.

Formula for Spring Pitch:
(L – 3d) ÷ Na = p
L = Length
d = Wire Diameter
Na = Active Coils
p = Pitch
Example:
  • [1 – ( 3 x 0.038)] ÷ 4 = p
  • (1 – 0.114) ÷ 4 = p
  • 0.886 ÷ 4 = p
  • 0.222 = p

Diagram

Closed And Squared Ends Spring PitchClosed And Squared Ends Spring Pitch

Closed and Ground

This end type also has two closed coils as ends but these are ground for the spring to stand up vertically straight. In the previous formula, we had to subtract 3 wire diameters from the free length. In this case, since half of the wire has already been ground off, it is no longer dead space taking up our free length. This means that we will only subtract two wires from the free length and then divide the result by the active coils.

Formula for Spring Pitch:

(L – 2d) ÷ Na = p

  • L = Length
  • d = Wire Diameter
  • Na = Active Coils
  • p = Pitch
Example:

Based on the given formula. The example shown below demonstrates how to calculate your compression spring's pitch.

  • [1 – ( 2 x 0.038)] ÷ 4 = p
  • (1 – 0.076) ÷ 4 = p
  • 0.924 ÷ 4 = p
  • 0.231 = p

Diagram

Closed And Ground Ends Spring PitchClosed And Ground Ends Spring Pitch

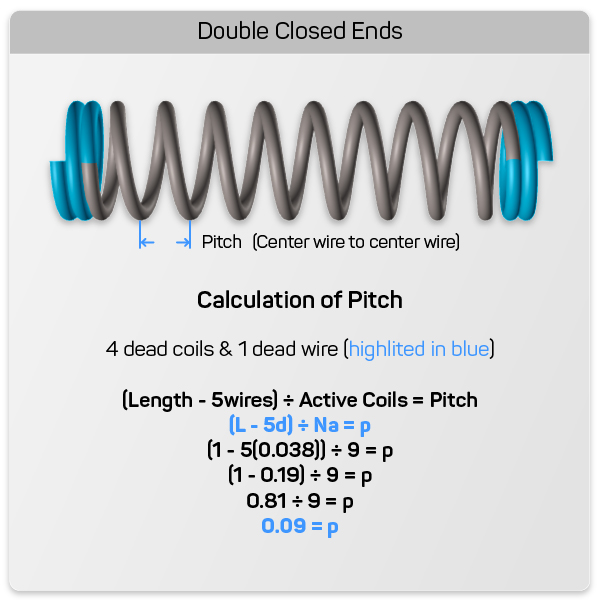
Double Closed Ends

For double closed ends, you must follow the same formula as you did for closed and squared ends except now we have two more closed (dead) coils. This means that you will subtract 4 dead coils and 1 dead wire from the free length. Giving you a total of 5 wire diameters subtracted from the free length, divided by the active coils. The formula below explains this concept.

Formula for Spring Pitch:

(L – 5d) ÷ Na = p

  • L = Length
  • d = Wire Diameter
  • Na = Active Coils
  • p = Pitch
Example:

Based on the given formula. The example shown below demonstrates how to calculate your compression spring's pitch.

  • [1 – ( 5 x 0.038)] ÷ 4 = p
  • (1 – 0.190) ÷ 4 = p
  • 0.810 ÷ 4 = p
  • 0.203 = p

Diagram

double closed ends spring pitchdouble closed ends spring pitch

Open Ends

Open ends don’t have any closed or dead coils. The measurement of spring pitch remains from center of wire to center of wire though. This means that you will still have to subtract one wire diameter from the free length before you divide the free length by the total coils. Follow the formula below to calculate the spring pitch of a coil spring with open ends.

Formula for Spring Pitch:
(L – d) ÷ Na = p
  • L = Length
  • d = Wire Diameter
  • Na = Active Coils
  • p = Pitch
Example:

Based on the given formula. The example shown below demonstrates how to calculate your compression spring's pitch.

  • (1 – 0.038) ÷ 4 = p
  • 0.962 ÷ 4 = p
  • 0.241 = p

Diagram

Opend Ends Spring PitchOpend Ends Spring Pitch

Invest in precision and quality

Spring Creator 5.0 offers you the possibility to design springs that perfectly fit your needs. Our platform not only allows you to design various types of springs but also provides advanced tools like the Online Spring Force Tester to simulate and evaluate spring performance. Visualize your design in 3D, download detailed blueprints, and get instant quotes. Try it for free and discover why we are the preferred choice of engineers and makers!

Spring Creator tool - Try it now

Created by Alfonso Jaramillo Jr

President Acxess Spring

Over 40 Years of Experience in Spring Engineering and Manufacturing